背景
最近又遇到了AC自动机,顺便复习了一下以前学过的KMP算法,两者其实具有很相似的结构,因此写篇文章总结一下。
KMP算法
问题
KMP算法解决字符串模式匹配问题,给定字符串s和p,计算s中出现p的位置,p即pattern。实际上单就这个问题而言,完全可以采用暴力匹配的方式,假设s的长度为m,p的长度为n,则暴力匹配的时间复杂度为O(mn),相比之下,KMP算法的时间复杂度为O(m+n)。
s: abxcabcycabcc
p: cabcc
一些定义
先定义一些东西,方便后面阐释KMP算法背后的思想。
定义1:
- 前缀 prefix:字符串a是字符串b的前缀,意味着a是b的子串,且出现在开头。
- 后缀 suffix:字符串a是字符串b的后缀,意味着a是b的子串,且出现为尾部。
"abc" is prefix of "abcdefg"
"efg" is suffix of "abcdefg"
在本文中,我们只考虑真子串的情况,虽然按照定义,任意字符串自身也是自身的前缀,但这对于KMP来说没有意义。现在,我们可以定义一个有趣的东西:给定字符串s,如果字符串r既是s的前缀,也是s的后缀,它就是s的公共前后缀。
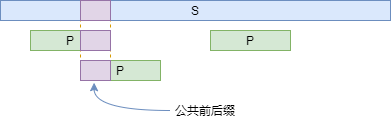
如上图,当我们用模式p匹配字符串s时,如果s中多次出现的p存在重叠的情况,那么重叠部分其实就是p的一个公共前后缀。
然后我们可以发现公共前后缀的两个有趣的性质:
性质:
- 如果字符串r1,r2是s的两个不同的公共前后缀,且len(r1)>len(r2),则r2是r1的公共前后缀。
- 设s[0:i]的最长公共前后缀为s[0:k],则s[0:k-1]必然是s[0:i-1]的一个公共前后缀。
这两个性质其实很trivial,读者自己画个图就能理解了,我懒得画图了,通过上面的性质1,我们很容易可以得出下面的结论:
引理1:
- 设$r_1,r_2…$是不同的字符串,$r_{i+1}$是$r_{i}$的最长公共前后缀,且$r_1$是$s$的最长公共前后缀,则$r_1,r_2…$依次是$s$长度递减的所有的公共前后缀。
next数组
现在我们先不谈KMP算法,先计算一个数组next,它的长度等于字符串p的长度(即pattern的长度),这个数组是这么定义的:
定义2:
- next[k]是p[0:k]的最长公共前后缀的长度,也即p[0:k]的最长公共前后缀为p[0:next[k]-1]。特别地,next[0]=0。注意:这里的p[0:k]是闭区间。
vector<int> make_next(const string& p) {
vector<int> next(p.size(), 0);
int i = 0, j = 1;
while (j < p.size()) {
while (p[i] != p[j] && i > 0) {// 根据引理1,按长度递减的顺序尝试所有可能的p[0:i-1]的公共前后缀
i = next[i - 1];
}
if (p[i] == p[j]) {// 找到了匹配的p[i]和p[j],则p[0:j]的最长公共前后缀为p[0:i]
next[j] = ++i;
} else {
next[j] = 0;// 否则为0
}
j++;
}
return next;
}
上面的代码计算next数组。实际上,循环中维护了如下的不变式:
p[0:j-1]的最长公共前后缀为p[0:i-1](i=0时特殊处理),且next[0:j-1]已ready。
当前循环的目标就是计算p[0:j]的最长公共前后缀,根据性质1,它等于p[0:j-1]的某一个公共前后缀加上p[j],那显然我们要从p[0:j-1]的最长公共前后缀p[0:i-1]开始长度递减地尝试,如何按长度递减呢,参照引理1,我们只需迭代地拿p[0:i-1]的最长公共前后缀即可(这已经由next数组提供了)。
上面的思想在代码中的体现就是内层的while循环,经过while循环后只有两种结果,一是我们找到了一个最长的合适的p[0:j-1]的公共前后缀p[0:i-1],且p[i]=p[j],此时我们可以宣布,p[0:j]的最长公共前后缀就是p[0:i],否则,就说明p[0:j]没有最长公共前后缀。
我们再分析一下上面算法的复杂度,注意到i和j都是整数,且循环内部变量i的增加必然伴随着j的增加,而j最多增大到len(p),因此i的减少最多出现len(p)次,从而内部循环次数不超过2len(p),时间复杂度为O(len(p))。
算法主体
终于可以开始介绍KMP算法的本体了:
vector<int> kmp(const string& s, const string& p) {
vector<int> res;
if (s.size() < p.size()) return res;
int i = 0, j = 0;
auto next = make_next(p);
while (i != s.size()) {
while (s[i] != p[j] && j > 0) {
j = next[j - 1];
}
if (s[i] == p[j]) {
i++; j++;
} else {
i++;
}
if (j == p.size()) {
res.push_back(i - p.size());
j = next[j - 1];
}
}
return res;
}
依然通过循环不变式的思路来分析算法,这个循环维护了这样一个不变式:
p[0:j-1]是p的所有前缀(这里包括p自身)中与s[i-j:i-1]匹配的最长的一个前缀。
那显然,我们按i走完一遍循环,一定能够把p在s中出现的所有位置给找到,因为只要出现了,p本身就会是最长前缀。现在我们看如何维持这个不变式,其实和计算next数组的方法很相似。
我们还是尝试匹配p[j]和s[i],如果不匹配,由于p[0:j-1]已经和s[i-j:i-1]匹配好了,此时我们看p[0:j-1]的最长公共前后缀p[0:next[j-1]-1],它也必然和s[i-next[j-1]:i-1]匹配好了,这说明我们可以直接尝试用p[next[j-1]]和s[i]尝试匹配,这是除p[0:j-1]以外最长的可能的前缀;如果还不匹配,迭代下去即可。
算法的时间复杂度分析与next数组构建异曲同工,j的增加依赖于i,而j最小为0,最高不超过i增加的次数,而i最大为len(s),因此循环次数上线为2len(s),从而复杂度为O(len(s))。加上make_next的O(len(p)),整个KMP算法的时间复杂度为O(len(s)+len(p))。
可以看到KMP算法的时间复杂度是线性的,但是我们可以看C++,Python等语言为字符串类实现的find方法,都没有采用KMP,而是使用传统的暴力搜索。这是因为KMP算法需要额外分配空间去计算前缀数组,在字符串较小的时候其实是不如直接暴力搜索的。KMP算法适用于对于一个固定的模式,需要对大量字符串进行匹配的情况,此时计算好next数组后我们就可以直接快速进行线性匹配。
AC自动机
问题
实际上在生产环境我们遇到的多数字符串模式匹配问题都是多模式匹配,即给定一系列字符串$p_1, p_2…p_k$,和字符串$s$,寻找$s$中出现任意$p_i$的位置。这个问题如果用KMP来解决的话,我们需要首先为每个p计算好next数组,然后依次匹配,构建部分的时间复杂度为O(len(p1)+…len(pk)),匹配部分的时间复杂度为O(k*len(s))。
而使用AC自动机的话,时间复杂度会是O(len(s)+len(p1)+…len(pk)+z),其中z是s中出现任意模式的总次数。
算法
构建Trie
AC自动机说是自动机,实际上整体构建在一棵Trie上,因此我们首先定义数据结构如下:
class AcMatcher {
public:
AcMatcher(): root(new node()) {}
~AcMatcher();
void Add(const string &);
vector<string> Match(const string &);
void Build();
private:
struct node {
vector<node *> kids;
bool flag;
node *suffix;
node *dictSuffix;
node *parent;
char ch;
int depth;
node(char ch = '\0') : kids(256, nullptr), flag(false), suffix(nullptr), dictSuffix(nullptr), parent(nullptr), ch(ch), depth(0) {}
};
node *root;
};
我们先只看node结构,关注kids和flag,就是一棵标准的Trie树,flag为true表示当前结点是一个单词的结尾,kids为孩子结点。在本文中我们简化问题,仅考虑ASCII字符串,因此kids为长度256的数组。如果要支持unicode编码,kids就需要用哈希表来存储了。
此外,我们额外记录结点的深度depth和父亲结点的指针parent,以及当前结点表示的字符ch。另外两个成员suffix和dictSuffix先按下不表。
先实现一下Add函数,Add单次添加一个模式字符串,并扩充Trie树,非常简单:
void AcMatcher::Add(const string &s) {
auto p = root;
for (auto ch : s) {
if (!p->kids[ch]) {
p->kids[ch] = new node(ch);
p->kids[ch]->parent = p;
p->kids[ch]->depth = p->depth + 1;
}
p = p->kids[ch];
}
p->flag = true;
}
构建自动机
构建完Trie树后,我们再来看suffix和dictSuffix是什么:
上图顺着黑色箭头形成一棵Trie树,树中存储了a, ab, bab, bc, bca, c, caa这些字符串,蓝色结点表示flag为true。Trie树中任意结点均代表某一个模式字符串pi的前缀字符串,对于结点q,其代表的字符串称为s(q),我们定义:
- suffix:
q->suffix指向当前Trie树中存在的s(q)的最长真后缀所在结点。如果不存在这样的结点,则指向root。
在图中,蓝色箭头表示suffix的指向。例如,bab的最长真后缀为ab,其恰好在Trie树中存在,因此直接指向ab所在结点。再比如,caa的真前缀依次为aa,a,但Trie树中存在的前缀仅有a,因此按照定义,其指向a。
看完这个定义,我们显然可以得出一个结论:只要顺着结点q的suffix一路走下去,直到root,就会遍历整棵Trie树中出现的q的所有真后缀。这点和KMP算法中使用最长公共前后缀有异曲同工之妙。
那么dictSuffix是什么呢?其实就是顺着suffix走下去遇到的第一个蓝色结点,严格一点说比较绕:
- dictSuffix:
q->dictSuffix指向当前Trie树中存储的所有模式字符串pi中,是s(q)前缀的中的最长的那个。如果没有就指向nullptr。
二者的计算都可以通过BFS的形式一遍过,因为suffix一定是指向深度较小的结点,BFS保证深度较小的结点已经计算过了,这相当于树上的DP(而KMP是在数组上计算类似的东西):
void AcMatcher::Build() {
queue<node *> q({root});
while (!q.empty()) {
auto p = q.front(); q.pop();
if (p->parent) {
auto pb = p->parent->suffix;
while (pb) {
if (pb->kids[p->ch]) {
p->suffix = pb->kids[p->ch]; break;
} else {
pb = pb->suffix;
}
}
if (!p->suffix) p->suffix = root;
pb = p->suffix;
while (pb) {
if (pb->flag) {
p->dictSuffix = pb; break;
} else {
pb = pb->dictSuffix;
}
}
}
for (auto kid : p->kids) if (kid) q.push(kid);
}
}
上面的代码中,先计算suffix,计算好后就可以用于dictSuffix的计算了,suffix的计算通过迭代地寻找父亲的suffix,而后看父亲的孩子中是否存在当前的字符即可,如果没有,就看父亲的suffix的suffix(也就是遍历了树中父亲的所有可能的真后缀),非常简单。
匹配
现在我们看一下匹配的算法:
vector<string> AcMatcher::Match(const string &s) {
vector<string> res; char c; auto p = root;
for (int i = 0; i < s.size(); i++) {
c = s[i];
while (p && !p->kids[c]) p = p->suffix;
if (!p) {
p = root; continue;
}
p = p->kids[c];
auto t = p;
while (t) {
if (t->flag) res.push_back(s.substr(i - t->depth + 1, t->depth));
t = t->dictSuffix;
}
}
return res;
}
我们依然以循环不变式的角度分析这段代码的正确性,这个循环维护了如下的不变式:
- p是s[0:i-1]的在Trie树中的最长后缀。
那么整个循环中的代码就是在计算s[0:i]在Trie中的最长后缀,并让p指向它。我们看下循环的前6行,是不是这样?如果p的孩子中有s[i],那显然p直接指向这个孩子即可,因为既然当前指向s[0:i-1]的最长后缀,那么指向p的孩子后就会是s[0:i]的最长后缀;如果p的孩子中没有匹配的s[i],那么只能退而求其次寻找p的suffix,然后看这个suffix的孩子了,以此类推。如果最终没有找到任何后缀,说明s[0:i]在Trie树中没有任何后缀,p指向root。
那么这个不变式有什么用呢?看循环的最后5行,以为对于p来说,在这5行中,p已是s[0:i]的最长后缀,通过遍历p及其suffix,我们就会找到s[0:i]在Trie树中的所有后缀,这些后缀字符串中的蓝色结点就代表着s[0:i]的一个子模式匹配。而这恰好被dictSuffix预先计算好了,因此我们只要按dictSuffix遍历,而不需要用suffix(后者需要的遍历次数更多),遍历中遇到的所有结点代表的字符串就是所有在s[i]处的匹配的模式字符串了。
下面来看一下匹配过程的时间复杂度,这个复杂度分析与KMP有点类似,我们关注p的深度,即depth,深度的增加仅可能伴随着i的增加,因此最多p下钻到len(s)的深度,而在第一个循环中p转移到p->suffix的过程深度是减小的,这也是个离散的过程,因此减小的次数不会超过len(s),再看最终输出去时候对dictSuffix的遍历次数,其实总和等于子模式在s中出现的次数z,从而复杂度为O(len(s)+z)。可以看到如果出现的次数不多,AC自动机的时间复杂度是线性于输入字符串长度的,这非常牛逼。

